Poker: A Guaranteed Income for Life

Next Page | Contents | The Precursors to Neo-Tech | Previous Page

3. Hypnosis (87)

Because the good player is able to intensely study and closely scrutinize each poker opponent, he quickly gets to know their minds and psyches. With planned experiments, he can discover subconscious responses in many players and then actually hypnotize certain players--particularly the dull, emotional, or mystical ones. Typical hypnotic stimuli are--

• staring into the subject's eyes (psychological)
• moving a finger through the pot (visual and motion)
• breathing audibly during a tense silence (sound)
• tapping fingers on the table (sound and motion)
• repeating sub audible chant-like commands (e.g., "fold--fold--fold," or "raise--raise--raise").

Various repeated motions, sounds, or muffled voices can subconsciously instruct or signal vacillating opponents to make specific folds, calls, bets, or raises. The alert player can discover subconscious or hypnotic signals that will trigger automatic or trained reactions in his opponents.

While the good player can get certain opponents to bet, call, or fold by hypnosis, he uses hypnotizing actions cautiously to avoid revealing his own hands and intentions to alert opponents.

After the draw, John Finn takes the final raise for $100. He has Scotty Nichols beat and wants him to call. Scotty groans. Looking at the huge pot, he sees John's finger slowly stirring the pile of money--stirring slowly and smoothly. Ten and twenty-dollar bills are moving in circles. Scotty's floating brown eyes start rotating with the money. His chubby hand slowly picks up a $100 bill. He calls the bet.

Scotty tries to smile as John pulls in the pot. Eventually he may become aware of that hypnotic trick. But then John will simply use another trick.

John estimates his earnings per life of hypnotic trick range from several hundred to several thousand dollars.

4. Distractions (88)

The good player can exploit his opponents more easily when they are distracted. A radio or television for sporting events has excellent distraction value. A late newspaper is usually good for several hands of distracted play from opponents checking horse-race results, the stock market, and the news. Pornographic literature offers an absorbing distraction. Good spreads of food and assorted drinks provide steady and effective distractions.

Availability of beer and liquor usually benefits the good player. One drink takes the sharpness off a player's ability to think and concentrate. Even a single beer will reduce the effectiveness of a superior player. That is why the good player never drinks before or during the game. And that is why the good player is glad to see superior-playing opponents take a drink.

Moderate amounts of alcohol have less effect on poor players because their concentrations are already at reduced levels. The poor player must drink enough to become intoxicated before his edge odds are reduced to even lower levels. But the advantages of having intoxicated opponents are sometimes canceled by disadvantages such as slowing down the game and causing drinking problems that may drive profitable opponents from the game.

Each week, John Finn is a good fellow and brings beer to the game, along with the late evening paper containing the complete stock-market closings and horse-race results. Ted and Sid read this paper while playing their hands. Every now and then they lose a pot to John because of that distraction.

Those newspapers cost John less than $15 per year, but are worth about a $1000 a year in distractions--or about $20 per newspaper.

By encouraging and creating distractions, John Finn increases everyone's confusion. At the same time, he keeps the action moving. In the Monday night game, however, he discovers his opponents will play for significantly higher stakes when using cash rather than faster-moving poker chips. (In most games, the reverse is true, and thus the good player normally prefers using poker chips.) To offset this, John speeds up the game by alternating two decks of cards between each shuffle and deal.

By using an array of distractions, John increases his edge odds by about 20 percent. That means $8000 additional income per year at his current winning rate. He estimates that while playing their hands, his opponents are distracted 35 percent of the time. And they are distracted a much higher percentage of the time when they are not involved in the action. The chart on page 142 estimates the in-action distractions of each player:

Time Distracted, %
(when in action)

5. Agreements (89)

The good player sometimes makes profitable agreements with other players. Occasionally, he can make an agreement with a loose player whereby each time either one wins a pot he will pay the other, for example, $5. Such an agreement will give the good player a guaranteed side income. Even when the loose player is a big loser, he will usually win more pots than the good player. Many poor players will gladly make such an agreement because they erroneously believe that a winner must win more pots than a loser. Also, most losers desire an association with a winner (the good player); such an association boosts their self-esteem by making them feel they are on the same level as the winner. Often a loose player happily maintains such an agreement indefinitely without ever admitting or even realizing that he is providing the good player with a steady side income.

Compared to John Finn, Sid Bennett plays more then twice as many hands, wins about 50 percent more pots, but loses nearly three times as often. He eagerly accepts John's suggestion that they pay each other $5 every time one of them wins a pot. Two years later, Sid is still pleased with this arrangement as indicated by his comments:

"At least I keep collecting these side bets," he says with a broad smile as John wins a huge pot and gives him $5. "Don't understand why you made such a stupid bet."

"Ha!" Quintin Merck snorts. He knows John makes money from the agreement. John knows it too, and his notebook data prove it:

The Sid Bennett Agreement

XVIII
Money Extraction (90)

The good poker player is involved in a long-term process of extracting maximum money from the game as well as from each individual player.

1. Winning Too Fast (91)

Money extraction at the maximum rate is not always in the best long-term financial interest of the good player. Uncontrolled maximum money extraction can cause the following problems:

• Players who would be long-term sources of important income may quit the game.
• Stakes or rules may be disadvantageously changed.
• Unfavorable attitudes may develop.
• Game may break up.

To extract maximum money, the good player often decreases his winning rate in order to control the flow of money. In other words, maximum-money extraction over the long term may require a slower winning rate.

2. Uncontrolled Money Flow(92)

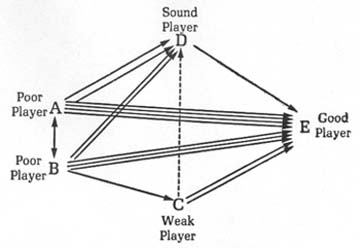
Over a period of many games, uncontrolled money flows in a pattern similar to that illustrated by the top diagram on the Money-Flow Pattern chart shown after Table 26. As the good player accumulates performance data on each player, these money-movement patterns become increasingly obvious.

Data for uncontrolled money flow are tabulated in Table 26. Notice the heavy losses absorbed by poor players A and B compared to players C and D. In that game, the good player, E, is extracting winnings through a natural, uncontrolled money flow. But poor player A may quit, for example, because continuous losses hurt his pride. And poor player B may insist on lower stakes because his sharp losses are causing him financial problems. The good player may be risking his future earnings unless he alters the money flow to a controlled pattern similar to that illustrated by the bottom diagram of that Money-Flow Pattern chart.

TABLE 26
UNCONTROLLED MONEY FLOW FOR TEN GAMES
Dollars Won (+) or Lost (-), $

^* Average winnings or losses for all the irregular players combined.

⁺ Averages are calculated by dividing the number of games attended by each player into the net winnings or losses of that player.

⁺⁺ The biggest winner for each of the ten games averages plus $445 per game. Edge odds of the good player E, for example, are calculated as $262/$445 X 100 = 59%.

MONEY-FLOW PATTERNS

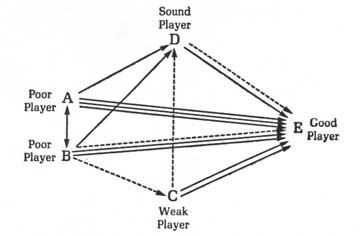
The ideal money-flow pattern for the good player occurs when he wins at the maximum rate each player can tolerate. That usually means winning less from the poorest players and more from the better players.

3. Controlled Money Flow (93)

The good player evaluates the money-extraction patterns on both a short-term and a long-term basis. If a controlled pattern seems desirable, he then determines how the money flow should be altered (extent and direction). In a controlled pattern, he usually extracts money more evenly from his opponents ... he extracts less from the poorer players and more from the better players. Controlled money flow shifts everyone's performance, as shown in Table 27.

TABLE 27
PERFORMANCE DATA

^* Average values for the irregular players.

That controlled pattern costs the good player an average of $22 per game. But if the money flow were not controlled, the continued heavy losses of poor players A and B could destroy the game, costing the good player his $17,400 winnings over those one hundred sessions. That $22 per session is his insurance premium for keeping the game going at high-profit conditions. The good player keeps performance records to determine the cost, value, and effectiveness of his control over the money flow. Money-flow control normally costs him 10-15 percent of his net winnings.

The good player usually takes control of the money flow during the early rounds, when his betting influence can be the greatest at the lowest cost. He alters the money-flow patterns by the following methods:

• He helps and favors the poorest players at the expense of the better players whenever practical.
• He drives the poor players out with first-round bets when a better player holds a strong hand. And conversely. he uses first-round bets to keep the better players in when a poor player holds a strong hand.
• He avoids, when practical, playing against a poor player after everyone else has folded in order to decrease his advantage over the poor player at a minimum cost. He also tries to make his least favorable plays (e.g., his experimental, image-building, and long-term strategy plays) against the poorest players.

John Finn spends some of his winnings to hold big losers like Sid Bennett and Ted Fehr in the game. The following data from John's records indicate that his insurance costs are profitable investments.

Without paying that insurance, John theoretically could have won $4500 more during that year. Yet without the insurance, the greater psychological and financial pressures on the big losers might have forced them to quit . . . and each big loser is worth much more than the entire $4500 insurance cost. Also, if several big losers had quit, the poker game could have been destroyed. John, therefore, considers the insurance cost an important and profitable investment.

How does he spend this $4500? The money buys him the valve that controls the money flow. He watches the losers closely. When they are in psychological or financial trouble and on the verge of quitting, he opens the valve and feeds them morale-boosting money until they are steady again.

Winning players are of little value to John. Since there is no need to help them or boost their morale, he keeps the valve closed tight on them. He may even spend money to drive them out of the game if they hurt his financial best interests.

John Finn never spends money on any player except to gain eventual profits.

Next Page | Contents | The Precursors to Neo-Tech | Previous Page

Disclaimer - Copyright - Contact

Online: buildfreedom.org | terrorcrat.com / terroristbureaucrat.com